Steinitz, Zermelo, and Elkies
By NM Dan Heisman
In the late 19th century World Champion Wilhelm Steinitz laid down the fundamental principles of positional play. A good summary of his work can be found at the Exton Chess Club site. Among the several important bases postulated, one was that a chess game begins in equilibrium and that a player would have to make a mistake in order to lose.
A corollary of Steinitz’ work is that a player can’t win a drawn game by making brilliant moves – a theoretically drawn game can only be won as a result of an opponent’s mistake. It may take a brilliant move to pinpoint that mistake and make it apparent, but the fundamental principle applies: in order for your game to get better, it required mistakes by your opponent.
To Steinitz’ great credit, the main part of his theory was proven about 20 years later by mathematician Ernst Zermelo, a pioneer in mathematical game theory. If I may paraphrase Zermelo for layman, he stated (among other applications) that for any finite, complete knowledge game (such as chess, go, or checkers), if the game has an initial position that is winning for one player, then the player who is winning will remain winning unless he makes a mistake, and if the game has an initial position that is theoretically drawn it will remain drawn unless one player makes a mistake. This result is basically the same as that one aspect of what Steinitz wrote, except that Steinitz implied that the initial chess position is drawn, while Zermelo extended this to any similar game, including those which begin with a forced win for one player.
I have written previously for The Skittles Room (at Chess Cafe: DH) the article Applying Steinitz’ Laws about some of the ramifications for practical play, including applications from his principle above and others. This time I would like to concentrate just on this one issue.
It is fundamental and important to note that in mathematical terms “better” means to go from a theoretical loss or draw to a win, or from a loss to a draw, assuming best play on both sides. Conversely, “worse” means to go from a win to a loss or draw, or from a draw to a loss. “Better” in this sense does not mean to control more space, obtain a better pawn structure, or even win material unless this changes the expected outcome for the better, assuming best play.
To borrow from the earlier article, the proof that one cannot make the position better by making a move is rather straightforward: since evaluation assumes best play, then the best move must leave the evaluation unchanged. In other words, if it is your move, then your position is only as good as your best move, and if you make that best move, you have reached the potential for your move and your position is no better. For example, if you are winning and make a move that checkmates, then your position is not better because before your move you could have checkmated, so administering the checkmate realizes the evaluation but does not improve it.
As another example, take the initial position of a game. Consider what happens when White plays 1.e4. Indeed, afterwards, White has more central control and more mobility for his pieces, but in return he has given up the move. If 1.e4 is White’s best move, then playing it has reached the potential of the position, nothing more, and his position has not improved. And if another move, say 1.d4, is eventually proven best a la Hans Berliner’s suggestion, then 1.e4 may in fact, from a practical standpoint, make the position slightly worse.
What is interesting about this argument is that often good chess players disagree, but good mathematicians don’t! My bachelor’s degree is in mathematics, but I am hardly a mathematician, so I called upon someone who is both a strong player and distinguished mathematician, Harvard Professor of Mathematics Noam Elkies. Professor Elkies, who has also achieved a USCF master’s title, has posted on his website a relevant paper “Zermelo and the Early History of Game Theory” by Ulrich Schwalbe and Paul Walker. Professor Elkies was kind enough to reply (and later review this article):
“As you can see from that paper, the result is indeed usually attributed to Zermelo (also one of the founders of modern mathematical logic) though the attribution may be imprecise. If you use the resulting perfect strategy to define the concepts of "won/drawn/lost position" then it is an immediate corollary that there is no move that can improve your position in the sense of transforming a lost to a drawn or won position, or a drawn position to a won one, and the same is true of what you describe as "Steinitz's conjecture" … This does not contradict the possibility of improving your position in the practical sense of raising the expected value (in the sense of probability) of the game when played between opponents of roughly the same strength as those actually at the board. Between perfect players, that expected value would be constant at 1, 1/2, 0 depending on the won/drawn/lost evaluation of the initial position; between humans the expectation may be quite different, and may change a lot over the course of the game.”
I could not have said it better myself – and that is the truth.
For the purposes of the following discussions let’s consider the math way of looking at this issue the “theoretical” way and the other way the “practical” way. Let’s begin by considering a fairly straightforward hypothetical case:
Suppose you have an endgame position where you are “winning” and have 30 different possible legal moves. Further, let’s assume that they break down the following way:
Then, in the theoretical sense, all 12 of the moves that win are “equally” best, although not, as Professor Elkies eloquently points out, in the practical sense. In fact, one or more of these 12 moves might be mate in one! This leads to a similar example which was recently suggested to me:
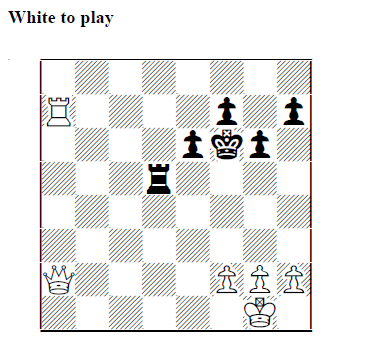
Assuming the game is not near the 50-move rule draw, White has no moves which lose or draw. So theoretically all moves are equally good but, from a practical standpoint, that is clearly not true. I would certainly not tell my students to play anything other than 1.Rb8#, the only mate in one in the position. But if White does not mate, his position has not gotten “worse” in the sense that he is winning anyway. A win is a win is a win.
I recently heard an anecdote about a game played by former World Champion Vladimir Kramnik. Apparently GM Kramnik was running short on time and found an easily winning line. After he won, someone pointed out a much quicker win, but Kramnik correctly noted that it would be impractical for him to spend time looking for an easier win once he found an easy win. It’s similar to the logic involved with the previous diagram.
Besides the corollary to Zermelo’s theorem about not being able to win a drawn position with a brilliant move, another corollary is that making a move that is not (equally) best can only deteriorate the position. We can consider this corollary two ways.
In the theoretical sense, playing a move other than 1.Rb8# in the previous diagram is not “inferior” since anything wins. However, in a practical sense delaying the win could result in further mistakes costing the win or a loss on time. For example, if White plays 1.Rbb7 this is not a theoretical blunder in the sense that White can still mate on the next move. He has not made an “inferior” move so his position did not deteriorate. 1.Rbb7 was theoretically “equal best” but clearly not as desirable as 1.Rb8# from a practical sense.
Now let’s return to the endgame where there were 30 moves and 12 of those won. If White plays any of those 12 then, theoretically, his position does not deteriorate (he can still win and that’s the best he can ever do) and, from that standpoint, all 12 are considered equally good. But if White does play an inferior move – one of the other 18 – then he can no longer force a win and his position has deteriorated, both theoretically and practically. So playing a move not (equally) best will, as conjectured, make the position worse.
Finally, here is a “technique” problem I often use:
By NM Dan Heisman
In the late 19th century World Champion Wilhelm Steinitz laid down the fundamental principles of positional play. A good summary of his work can be found at the Exton Chess Club site. Among the several important bases postulated, one was that a chess game begins in equilibrium and that a player would have to make a mistake in order to lose.
A corollary of Steinitz’ work is that a player can’t win a drawn game by making brilliant moves – a theoretically drawn game can only be won as a result of an opponent’s mistake. It may take a brilliant move to pinpoint that mistake and make it apparent, but the fundamental principle applies: in order for your game to get better, it required mistakes by your opponent.
To Steinitz’ great credit, the main part of his theory was proven about 20 years later by mathematician Ernst Zermelo, a pioneer in mathematical game theory. If I may paraphrase Zermelo for layman, he stated (among other applications) that for any finite, complete knowledge game (such as chess, go, or checkers), if the game has an initial position that is winning for one player, then the player who is winning will remain winning unless he makes a mistake, and if the game has an initial position that is theoretically drawn it will remain drawn unless one player makes a mistake. This result is basically the same as that one aspect of what Steinitz wrote, except that Steinitz implied that the initial chess position is drawn, while Zermelo extended this to any similar game, including those which begin with a forced win for one player.
I have written previously for The Skittles Room (at Chess Cafe: DH) the article Applying Steinitz’ Laws about some of the ramifications for practical play, including applications from his principle above and others. This time I would like to concentrate just on this one issue.
It is fundamental and important to note that in mathematical terms “better” means to go from a theoretical loss or draw to a win, or from a loss to a draw, assuming best play on both sides. Conversely, “worse” means to go from a win to a loss or draw, or from a draw to a loss. “Better” in this sense does not mean to control more space, obtain a better pawn structure, or even win material unless this changes the expected outcome for the better, assuming best play.
To borrow from the earlier article, the proof that one cannot make the position better by making a move is rather straightforward: since evaluation assumes best play, then the best move must leave the evaluation unchanged. In other words, if it is your move, then your position is only as good as your best move, and if you make that best move, you have reached the potential for your move and your position is no better. For example, if you are winning and make a move that checkmates, then your position is not better because before your move you could have checkmated, so administering the checkmate realizes the evaluation but does not improve it.
As another example, take the initial position of a game. Consider what happens when White plays 1.e4. Indeed, afterwards, White has more central control and more mobility for his pieces, but in return he has given up the move. If 1.e4 is White’s best move, then playing it has reached the potential of the position, nothing more, and his position has not improved. And if another move, say 1.d4, is eventually proven best a la Hans Berliner’s suggestion, then 1.e4 may in fact, from a practical standpoint, make the position slightly worse.
What is interesting about this argument is that often good chess players disagree, but good mathematicians don’t! My bachelor’s degree is in mathematics, but I am hardly a mathematician, so I called upon someone who is both a strong player and distinguished mathematician, Harvard Professor of Mathematics Noam Elkies. Professor Elkies, who has also achieved a USCF master’s title, has posted on his website a relevant paper “Zermelo and the Early History of Game Theory” by Ulrich Schwalbe and Paul Walker. Professor Elkies was kind enough to reply (and later review this article):
“As you can see from that paper, the result is indeed usually attributed to Zermelo (also one of the founders of modern mathematical logic) though the attribution may be imprecise. If you use the resulting perfect strategy to define the concepts of "won/drawn/lost position" then it is an immediate corollary that there is no move that can improve your position in the sense of transforming a lost to a drawn or won position, or a drawn position to a won one, and the same is true of what you describe as "Steinitz's conjecture" … This does not contradict the possibility of improving your position in the practical sense of raising the expected value (in the sense of probability) of the game when played between opponents of roughly the same strength as those actually at the board. Between perfect players, that expected value would be constant at 1, 1/2, 0 depending on the won/drawn/lost evaluation of the initial position; between humans the expectation may be quite different, and may change a lot over the course of the game.”
I could not have said it better myself – and that is the truth.
For the purposes of the following discussions let’s consider the math way of looking at this issue the “theoretical” way and the other way the “practical” way. Let’s begin by considering a fairly straightforward hypothetical case:
Suppose you have an endgame position where you are “winning” and have 30 different possible legal moves. Further, let’s assume that they break down the following way:
- 12 moves out of the 30 win with further best play on both sides (after the initial move)
- 8 of the 30 draw
- 10 of the 30 lose
Then, in the theoretical sense, all 12 of the moves that win are “equally” best, although not, as Professor Elkies eloquently points out, in the practical sense. In fact, one or more of these 12 moves might be mate in one! This leads to a similar example which was recently suggested to me:
Assuming the game is not near the 50-move rule draw, White has no moves which lose or draw. So theoretically all moves are equally good but, from a practical standpoint, that is clearly not true. I would certainly not tell my students to play anything other than 1.Rb8#, the only mate in one in the position. But if White does not mate, his position has not gotten “worse” in the sense that he is winning anyway. A win is a win is a win.
I recently heard an anecdote about a game played by former World Champion Vladimir Kramnik. Apparently GM Kramnik was running short on time and found an easily winning line. After he won, someone pointed out a much quicker win, but Kramnik correctly noted that it would be impractical for him to spend time looking for an easier win once he found an easy win. It’s similar to the logic involved with the previous diagram.
Besides the corollary to Zermelo’s theorem about not being able to win a drawn position with a brilliant move, another corollary is that making a move that is not (equally) best can only deteriorate the position. We can consider this corollary two ways.
In the theoretical sense, playing a move other than 1.Rb8# in the previous diagram is not “inferior” since anything wins. However, in a practical sense delaying the win could result in further mistakes costing the win or a loss on time. For example, if White plays 1.Rbb7 this is not a theoretical blunder in the sense that White can still mate on the next move. He has not made an “inferior” move so his position did not deteriorate. 1.Rbb7 was theoretically “equal best” but clearly not as desirable as 1.Rb8# from a practical sense.
Now let’s return to the endgame where there were 30 moves and 12 of those won. If White plays any of those 12 then, theoretically, his position does not deteriorate (he can still win and that’s the best he can ever do) and, from that standpoint, all 12 are considered equally good. But if White does play an inferior move – one of the other 18 – then he can no longer force a win and his position has deteriorated, both theoretically and practically. So playing a move not (equally) best will, as conjectured, make the position worse.
Finally, here is a “technique” problem I often use: